GNSS & Positioning

What is GNSS?

GNSS (Global Navigation Satellite System) is the umbrella term for satellite constellations that provide positioning, navigation, and timing (PNT) data. While GPS (Global Positioning System) is the most famous, it is actually just one of several systems operated worldwide. For official US government information, visit GPS.gov.

The Three Segments

• Space Segment: The constellation of satellites broadcasting signals.
• Control Segment: Ground stations that track satellites and upload orbital corrections.
• User Segment: A receiver (phone, car, survey gear) that calculates the position.

⚠️ Why is GPS Inaccurate?

Standard smartphone GPS is accurate to about 4.9 meters (16 ft). Why isn't it perfect? The signal travels 20,000 km and faces several hurdles:

🏙️ The "Urban Canyon" Problem

When you're in a narrow canyon—natural or urban—buildings or cliffs block large portions of the sky. Your GPS receiver may still get a position fix, but all the visible satellites come from the same narrow slice of sky, creating terrible geometry.

Limited Sky View: In a canyon, only a small portion of the sky is visible. All available satellites are clustered in this narrow window, leading to poor PDOP values.

Poor Geometry = Poor Accuracy: Even though you may lock onto 4+ satellites, if they're all from the same part of the sky, the trilateration "intersection zone" becomes elongated and uncertain.

💡 Real-World Example: This is why your phone's GPS often struggles in downtown Houston or Austin—the tall buildings create artificial canyons that limit sky visibility, just like being at the bottom of a natural canyon in Big Bend.

The 20-Minute Gap: Autonomy vs. Control

In GIS, we are used to real-time data. Google Maps updates traffic instantly. But deep space reintroduces the Time Lag.

The "Mars Delay": It takes up to 20 minutes for a radio signal to reach Mars. That means a 40-minute round trip for a "Yes/No" question.

"We can't rely on 'Ground Control' to read the test results. The device must be autonomous."

This forces a shift from Remote Control (Earth driving the rover) to Edge Computing (the rover driving itself). In the future of GIS, our sensors must be smart enough to analyze data before sending it home.

🎯 The Quest for the Centimeter (RTK)

For navigation, 5 meters is fine. For building a bridge, it is disastrous. Engineers use Real-Time Kinematic (RTK) to achieve 1 cm accuracy.

How it works:

1. Base Station: A receiver sits on a known coordinate and never moves. It calculates exactly how much the atmosphere is delaying the signal right now.
2. Correction Signal: It broadcasts this "correction" via radio or internet.
3. Rover: The mobile unit applies the correction instantly, removing the error.

Interactive: Trilateration Simulator

Drag the 3 satellites to see how their signal spheres overlap to pinpoint a location. Notice how poor geometry (satellites in a line) creates a larger area of uncertainty.

How Trilateration Works

The core math behind GPS is Trilateration. It's like a high-tech version of triangulation, but using spheres instead of triangles.

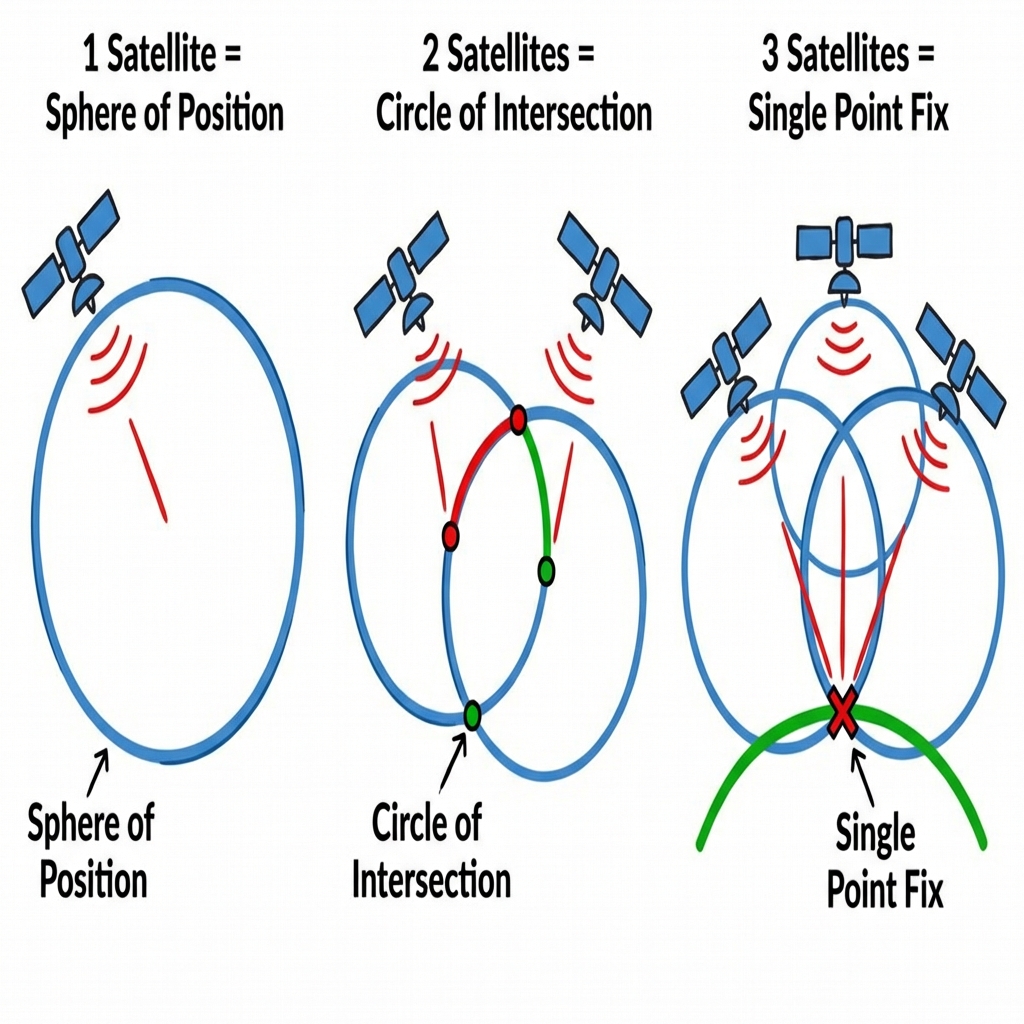
1. 1 Satellite: The location exists on a sphere of radius $R_1$ from the satellite.
2. 2 Satellites: The intersection of two spheres is a circle. The location exists on that circle.
3. 3 Satellites: The intersection of the circle and a third sphere narrows it down to two points. One is usually way out in space, the other is on Earth.
4. 4 Satellites: The fourth sphere resolves the ambiguity and corrects for time bias in the receiver's clock. TV + 3D Position.

🛑 Ethics: The "Strava" Problem

GPS creates a digital trail of your life. In 2018, the fitness app Strava released a "Heatmap" of user runs. It inadvertently revealed secret US military bases because soldiers were tracking their jogs around the perimeter. Location Privacy is a massive ethical issue in GIS.

⚠️ The Billion-Dollar Typo: The Negative Sign

Computers hate Degrees/Minutes/Seconds (DMS). They want Decimal Degrees (DD).

You must manually add the (-). The calculator won't do it for you!

Correct Coordinate: -97.51, 30.26 (Austin, Texas)

Summary of Big Ideas

• Trilateration: The mathematical process of finding the location by measuring distances to 4 or more satellites.
• Differential GPS (DGPS): Using a stationary base station at a known point to correct errors for a mobile receiver.
• DOP (Dilution of Precision): A measure of how much the satellite geometry (positions) affects positioning accuracy.
• Error Sources: Atmospheric delays, signal multipath (bouncing off buildings), and orbital drift.