Learning Objectives
- Explain the three segments of GPS
- Describe the principle of trilateration
- Understand why we need 4 satellites for a position fix
The Three Segments of GPS
1. Space Segment
- 31 operational satellites in Medium Earth Orbit (MEO)
- Orbiting in 6 orbital planes to ensure full Earth coverage
- Altitude: approximately 20,200 km above Earth
- Orbital period: ~12 hours (2 orbits per day)
- Each satellite carries atomic clocks (cesium and rubidium)
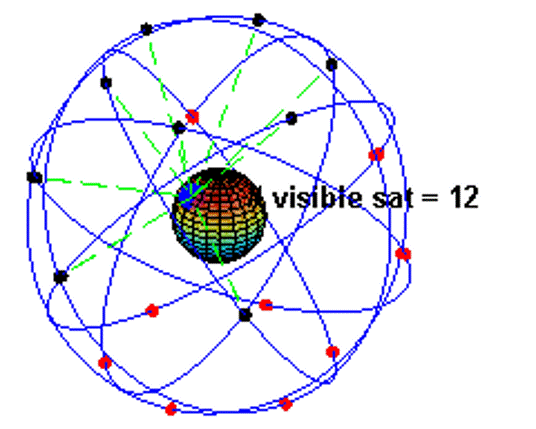
Peter H. Dana GPS Constellation Animation: Showing orbital paths and number of visible satellites (Source: GPSWorkshop)
Redundancy: At any time, about 8 to 10 satellites are visible above you. You only need four to get a position, but more satellites help if some are blocked by buildings or mountains.
2. Control Segment
- Master Control Station at Schriever Air Force Base, Colorado
- Monitor Stations worldwide tracking satellites
- Ground Antennas uploading navigation data to satellites
- Continuously updates satellite ephemeris and clock corrections
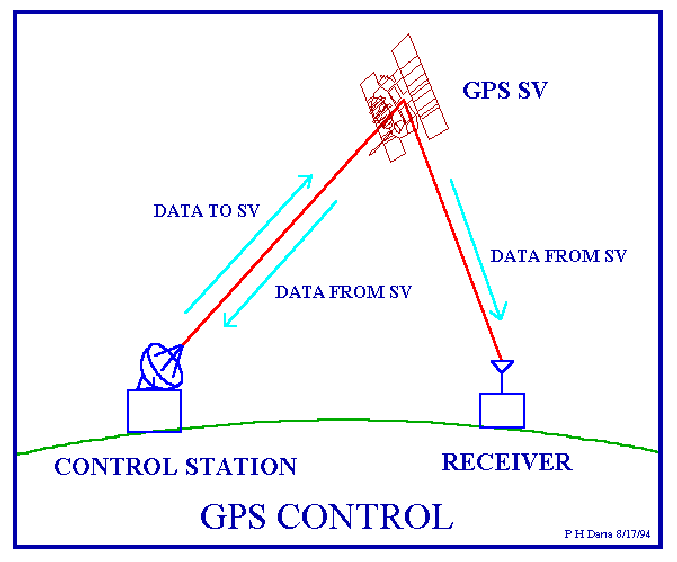
GPS Control Segment (Credit: Peter H. Dana)
3. User Segment
- All GPS receivers (your phone, car GPS, our Arduino units!)
- Receives signals from satellites
- Calculates position using trilateration
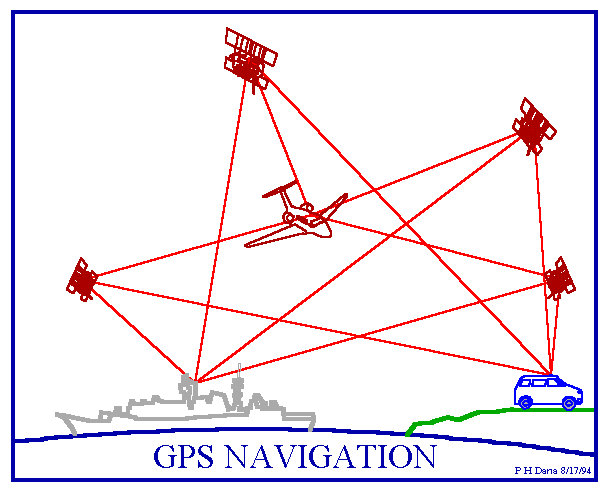
GPS Navigation Applications (Credit: Peter H. Dana)
GPS Signals
GPS satellites transmit on multiple frequencies:
| Signal | Frequency | Use |
|---|---|---|
| L1 | 1575.42 MHz | Civilian (C/A code) |
| L2 | 1227.60 MHz | Military (P code) + Civilian (L2C) |
| L5 | 1176.45 MHz | Safety-of-life applications |
Each signal contains:
- Pseudo-random noise (PRN) code - Unique identifier for each satellite
- Navigation message - Satellite position (ephemeris), clock corrections, almanac
Trilateration: How Position is Calculated
The Basic Principle
GPS determines position by measuring the distance from multiple satellites.
Satellites transmit their location and the precise time the signal left. The receiver calculates distance by measuring how long the signal took to arrive, traveling at the speed of light.
Example Calculation:
Speed of light: c = 299,792,458 m/s (about 300,000 km/s)
If signal travel time: t = 0.067 seconds
Distance = 299,792,458 m/s × 0.067 s = 20,086 km
That's about the altitude of GPS satellites!
The Clock Problem
Precise timing is critical. Satellites have atomic clocks, but receivers (like phones and our Arduino units) don't. How do we solve this?
Solution: We use a signal from a fourth satellite to synchronize the receiver's time!
The Colorado Example
Let's use a 2D example with cities in Colorado to understand how GPS finds your location:
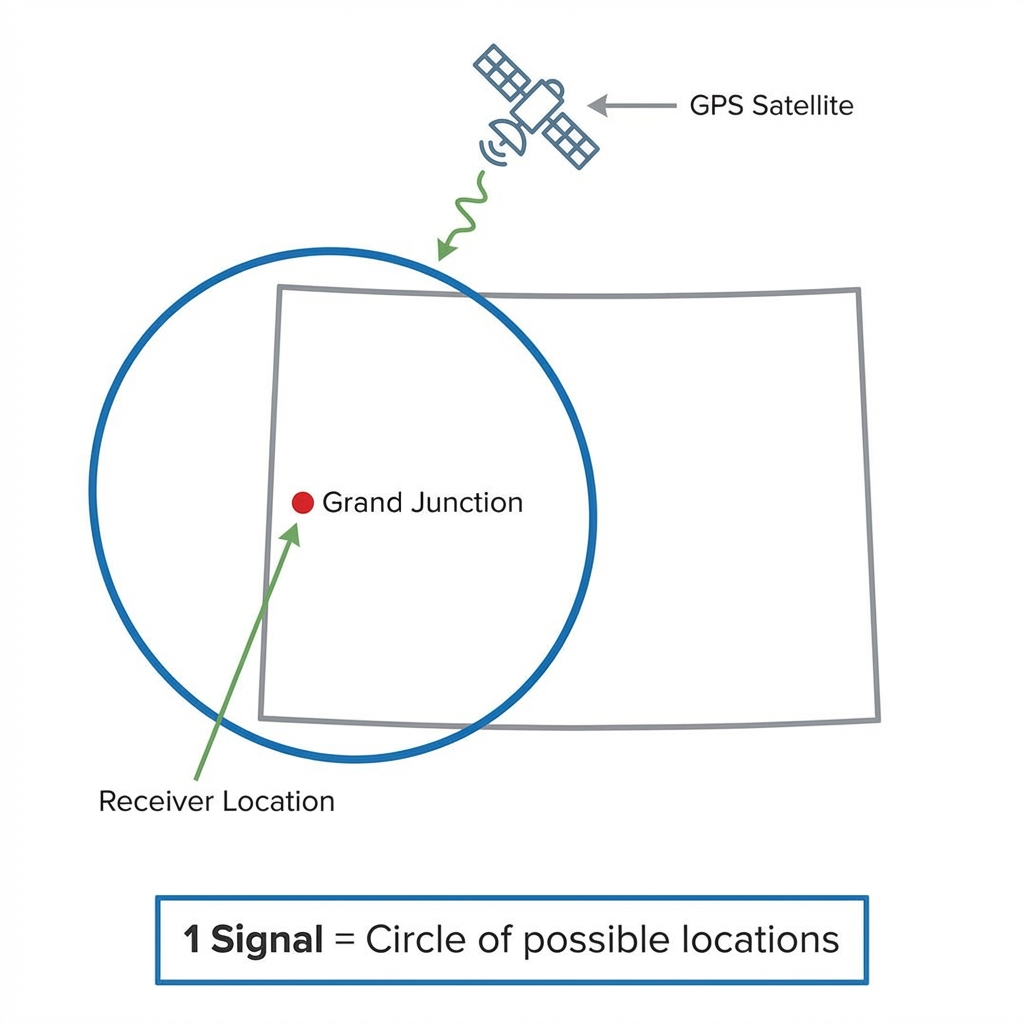
Step 1: One Signal
Knowing your distance from Grand Junction puts you anywhere on a circle around that point.
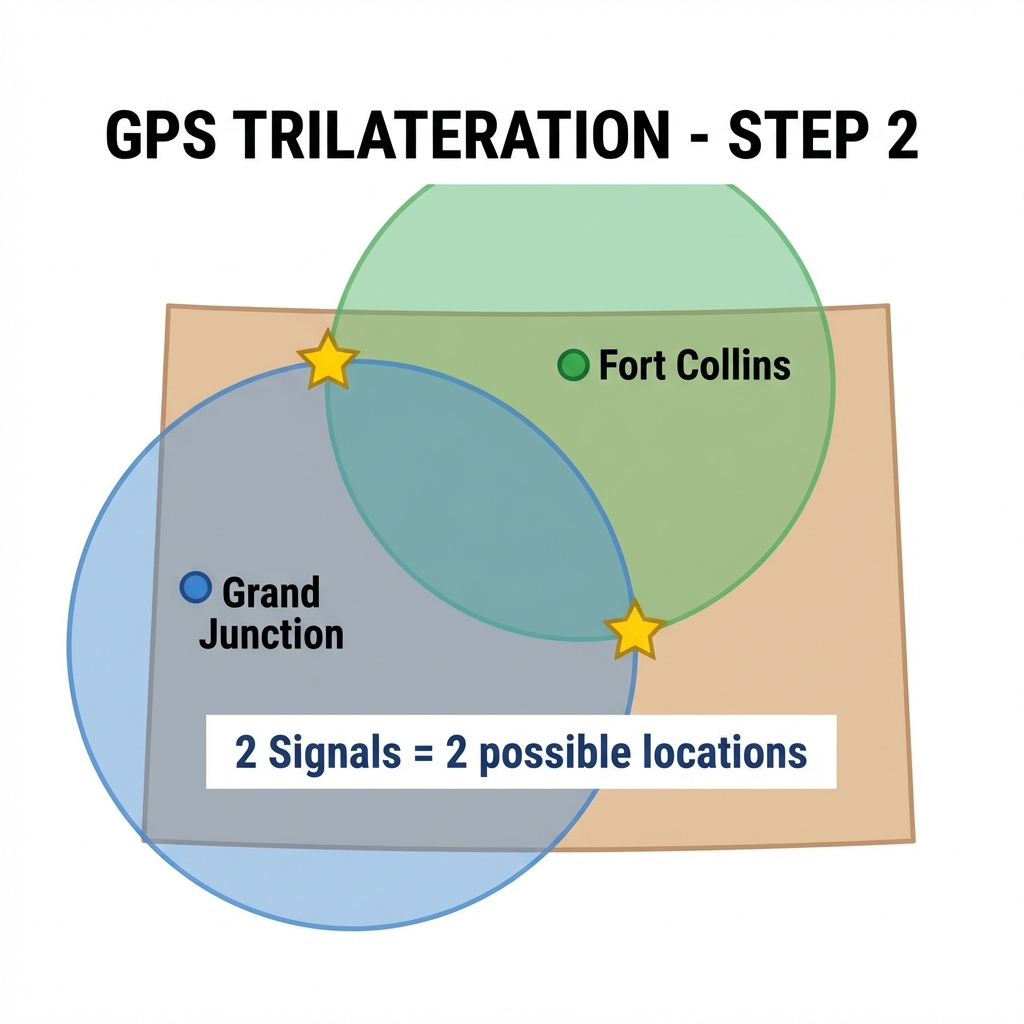
Step 2: Two Signals
Adding Fort Collins creates two intersecting circles, narrowing to two possible spots.
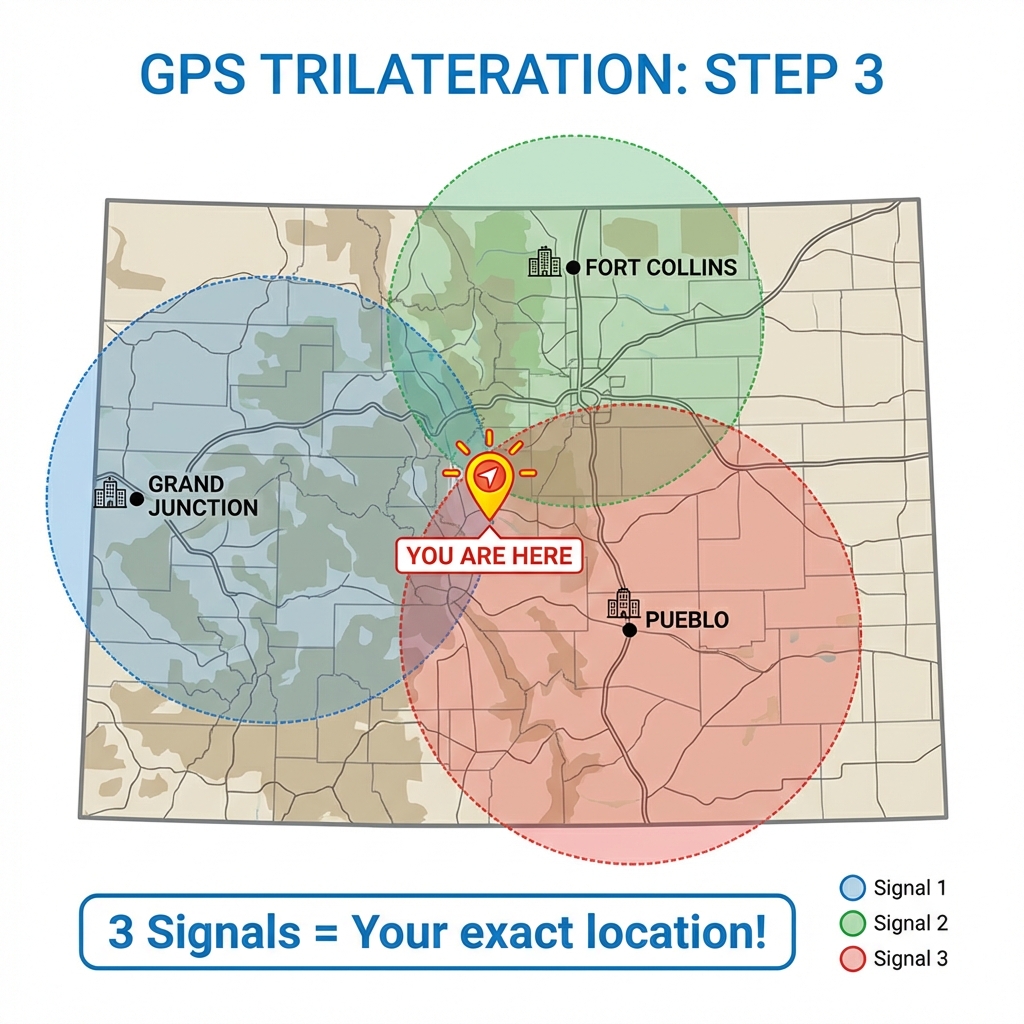
Step 3: Three Signals
A third point (Pueblo) intersects at only one location - that's YOU!
From 2D to 3D Space
In the real world, we extend the concept from 2D circles to 3D spheres. The following figures from the GIS&T Body of Knowledge illustrate this beautifully:
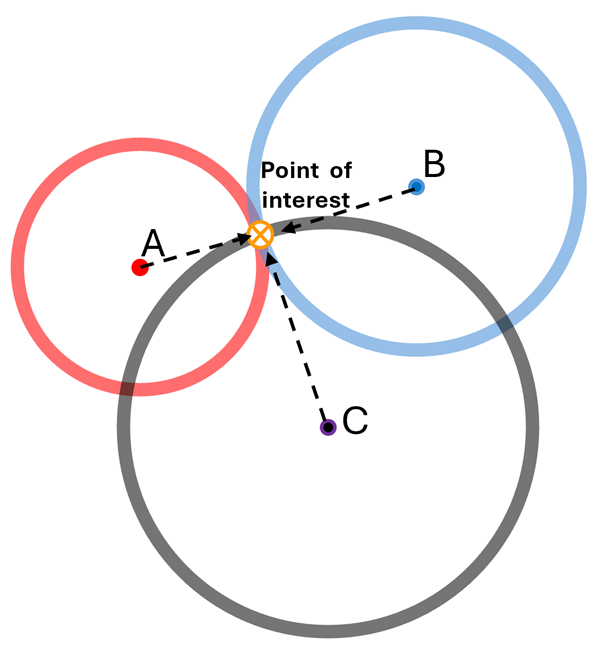
2D Trilateration
Three known points (A, B, C) create intersecting circles that meet at one unique point of interest.
Source: Hodgson, 2025 - GIS&T BoK
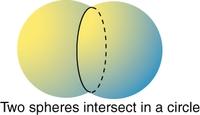
Step 4: Two Spheres
In 3D, two spheres from two satellites intersect to form a circle of possible locations.
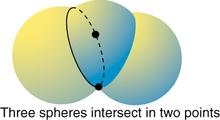
Step 5: Three Spheres
Adding a third sphere narrows the location to just two points where all three spheres meet.
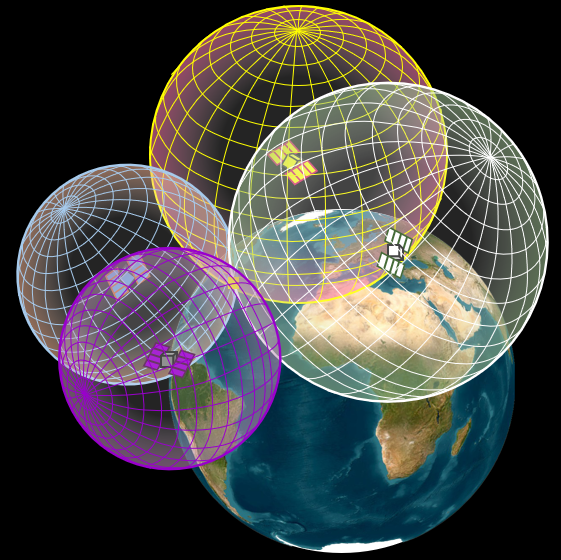
3D Trilateration
In 3D space, four satellites create intersecting spheres centered at each satellite position.
Source: Piovan in Hodgson, 2025
- Three spheres intersect at two points
- One point is usually far out in space or deep inside Earth
- The receiver knows to pick the point on the Earth's surface!
Why 4 Satellites?
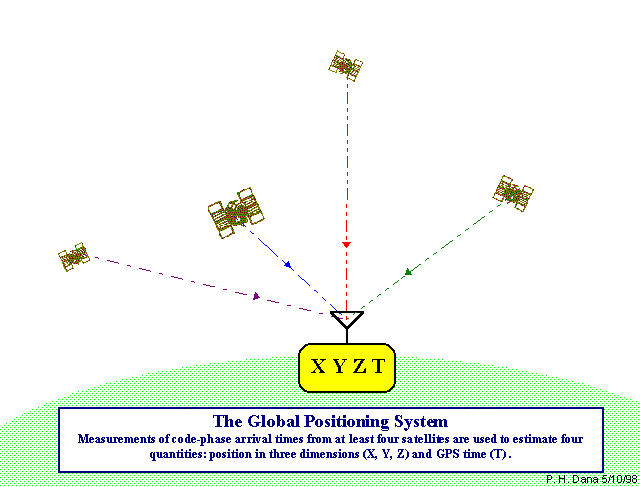
Four satellites estimate position (X, Y, Z) and time (T) (Credit: Peter H. Dana)
| # Satellites | What We Can Determine |
|---|---|
| 1 satellite | Distance sphere - somewhere on a sphere around the satellite |
| 2 satellites | Circle - intersection of two spheres |
| 3 satellites | Two points - intersection of three spheres |
| 4 satellites | One unique point + clock error correction |
The 4th satellite is crucial because our receiver clock is not as accurate as the atomic clocks on satellites. The 4th measurement allows us to solve for 4 unknowns: X, Y, Z position + receiver clock error.